Betting using standard deviation
Standard deviation can help bettors to predict betting outcomes. Let’s check out how to apply and calculate the standard deviation to your bets.
We revealed why bettors couldn’t depend solely on the mean, despite their propensity to be affected by outliers, and their inability to show dispersion within a number range.
There’re many ways that dispersion can be calculated, one of it is the standard deviation-a measurement, which expresses how much a group’s value varies from the group’s mean. Different metrics are either used directly for a function or distribution or are input parameters.

Normal Distribution against Poisson
Normal distribution defines continuous data with a symmetrical distribution, with a ‘bell’ shape characteristic.
Example: The mean length of time spent scoring a goal.
Poisson distribution explains how binary data are distributed from an infinite set. It usually model the count of an incident that occurs over a fixed time interval or at a fixed location.
Example: The number of times the player score a goal.
Predicting goals distributed around the English Premier League
Let’s take a look at the game goal differential in soccer as a test case. The difference in goal per match tends to be distributed normally. The difference in goal is the number of goals scored by the home team minus the goals scored by the team away, with nil leading to a draw.
English Premier League 2013/14 season data:
- Biggest home win: Manchester City vs. Norwich = 7 – 0
- Biggest away win: Tottenham vs. Liverpool = 0 – 5
- Mean goal difference: 0.3789 (mode and median = 0)
- Standard Deviation: 1.9188
There are many conclusions to be drawn from the results. The most common difference in the goal is mainly a draw, and the population is resembling symmetric, with a bias for home wins. We’ll focus on the standard deviation for now.
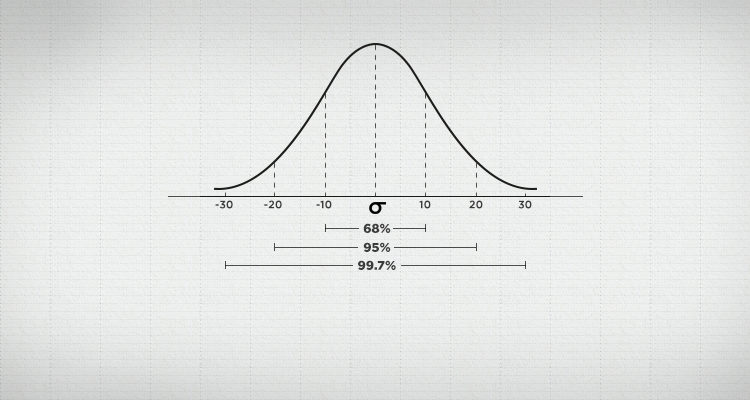
Measuring the Standard Deviation
To construct a standardized curve the normal distribution uses the two parameters (average and standard deviation). It’s about 68% of the distribution lies within a standard deviation away from the mean, and 95% lies within two standard deviations.
We estimate 68 % of the games to result between -1,5399 and 2,2977 goals in this case: (0,3789 + 1,9188). The continuous existence of the curve has its boundaries: -1.5399 difference in goals is not realistic.
To predict a home win by one goal difference, it is possible to shift one from a single (whole) value of 1, to reflect the continuous range between 0.5 and 1.5. In terms of standard deviations, we can then measure the variation from the mean for each value.
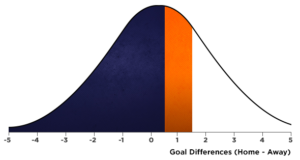
The best thing about this is that the normal distribution can now reconstruct, as shown. In this case, we will have to consider the region area shaded in orange.
The region shaded in blue is 52.15%, indicating the likelihood of less than one goal (or its continuous counterpart being less than 0.5 goals).
This calculation using most spreadsheet applications (in MS Excel: = NORM.DIST(0.5,0.3789, 1.9188,1). Similarly, the likelihood of targets below 1.5 is 72.05%. Therefore we estimate between these two values to be 19.53%.
We should have predicted 74.22 games out of 380 matches, thus finishing with the home team winning with only one goal difference. There were 75 matches, in fact, so it was very similar.
Repeating this for all variations in goals, we can distinguish the actual and approximate number of games, which ended up with distinct differences in goals.
The table below shows that the variance is small and that the normal distribution appears to be a good match-( there are ways to check for rationality, and this model suits well for data from the 2013/14 Premier League).
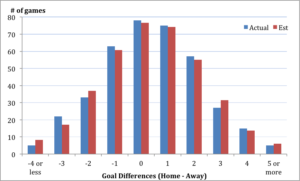
Suppose the spread for the EPL 2013/14 season is accurate now. So as a spread bettor, you may like to know what in the Premier League the chance of a home team winning by 1 or more goals is? Therefore, this is equal to 1-52.52%, which is 47.48%.
This is a standard calculation that relates in general to the EPL rather than to individual teams. In essence, bettors should be encouraged to find out data from particular teams rather than that of the Premier League generally.
Besides, the standard deviation is not only a measure of variance, because a higher value indicates more dispersion within a group; it is also an essential parameter for the calculation of probability, which is very useful for sports betting. We’ll concentrate on a future article on how a specific standard deviation will affect probabilities and distributions.