How frequently does the lead change during a game?
At any phase in a match, it is possible that one of the sides is up top or it’s a fair match with many of the changes happening each moment. Ever thought about how regularly that the lead of a match changes? Try not to put your cash on based only because your instinct is letting you know. We’re here to tell you why.
- Get to know the probabilities
- Figuring the chances of evening out
- Lead changes, but how regularly?
- Applying coin-tossing methods in your sports bet.

Get to know the probabilities
We make decisions by relying on probabilities each day, from planning around the weather or making a bet. Yet, as human beings, we make mistakes due to mislead of our natural instincts, but with statistics, our only ally trustworth enough to guide us right back on track.
Cautioning: The psychological trap uncovered right now so strange that it has astounded even the most refined analysts. Be that as it may, before we continue to the hypothesis, we should scrutinize our common impulses.
When there’s a matchup between two equaled skilled players. How frequently will the scoring lead change? What do you think the chances are when the count of the frames gets higher?
Since we expect equivalent expertise, we can utilize the most used randomizing trick, for example, the simple coin flip, and see how the leading player changes, by designating heads or tails to represent each of the players. For a leading scorer change to happen, the player who’s fallen behind requires to catch up in scores. So, let’s begin our simulation and see how often a take over will happen.
As we toss a coin for six times, getting six consecutive tails is hard and unlikely, Six tosses can generate 64 possible outcomes. The probability of getting six head or six tail in a roll is 2/64, or roughly 3%. (1 x ½ x ½ x ½ x ½ x ½)
On the other hand, we also understand that although each possible outcome has a 50% chance, it does not mean that six coin tosses equals 3 heads and 3 tails.
The correct probability of the equal number of heads and tails in a six coin flip is 20/64 (31%) or about ⅓. But even if we understand the calculation behind, this again does not mean that getting the equal number of 3 heads and 3 tails will appear once, if we flip 6 consecutive coins for 3 times.
Figuring the chances of evening out
First of all, the total number of tosses needs to be equal to have an equal outcome in any sequence. Once we have this equal, it’s time to figure out what are the chances of getting the same equal numbers of heads and tails.
Most of the common people are likely to think that, when the number of tosses increase, equal numbers of heads or tails become more likely, this is all based on applying the law of averages; as the sample size increases, the outcome is more likely to average out.
But this is incorrect.
In the book “Taking Chances” John Haigh tested the probabilities of heads and tails equalling out at any point in a sequence of independent tosses.
Coin Toss Probabilities:
| Probabilities of equal number of heads and tails | |||||
| Number of tosses | 2 | 4 | 5 | 6 | 10 |
| Chance of Equality | 1/2 | 3/8 | 5/16 | 35/128 | 63/256 |
| Probability | 50% | 37.5% | 31.25% | 27.34% | 24.6% |
The example that rises up out of the numbers is strange to such an extent, that the most intelligent among us take twice to accept and believe the information.The information shown that as the quantity of hurls builds the likelihood of evening out really diminishes.
On the off Chance that we continue flipping the coin for another 20 times, where should we be expecting Heads and tails to be equal? Very well may be at any of 2,4,6… tosses?, will it be a recent toss? One from the beginning? Or a toss near the middle?
Most of the people feel that the answer is somewhere near the middle, therefore statistical research has proven it is totally the opposite.
| Chances of last equality in a series of 20 coins at various times | ||||||
| Time of last equality | 0 or 20 | 2 or 18 | 4 or 16 | 6 or 14 | 8 or 12 | 10 |
| Probability | 17.62% | 9.27% | 7.36% | 6.55% | 6.17% | 6.06% |
This also means that, if the evening out is not happening early? It might take way longer for it to happen.
Lead changes, but how regularly?
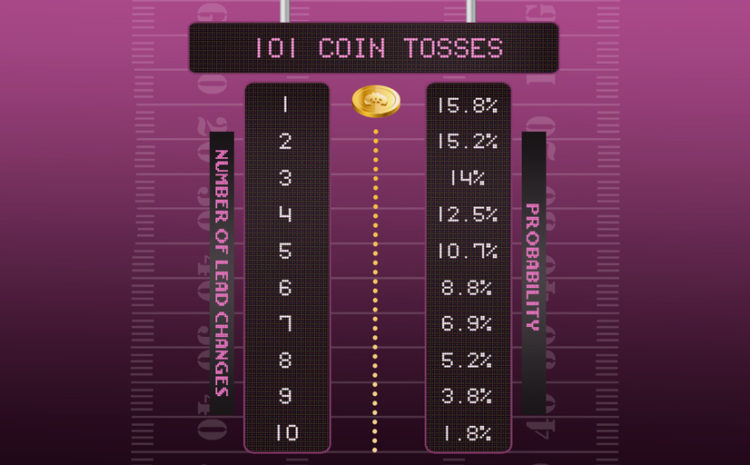
So how does the probability of evening out related to how often lead changes? Here’s a table of the probabilities, this clearly shows the chances of evening out in 101 coin tosses.
| Number of Lead Changes | Probability |
| 0 | 15.8% |
| 1 | 15.2% |
| 2 | 14% |
| 3 | 12.5% |
| 4 | 10.7% |
| 5 | 8.8% |
| 6 | 6.9% |
| 7 | 5.2% |
| 8 | 3.8% |
| 9 | 2.7% |
| 10 | 1.8% |
| 11 | 2.6% |
There’s only 32% chance of the lead change exceeding four times in a match. 5-9 change about 27% of the time, 4-5% changes 10+ times above.
The most interesting part is, 50% of the time the score did not equalize in the second half. This means the Head or tails was ahead after the halfway point, and will remain leading for the entire experiment.
Applying coin-tossing methods in your sports bet.
At this point, we should be clear on betting, by applying the experiment into betting. The entire experiment shows us among equally skilled players, if the match scores dont even out in a lengthy period of time, evening out the remaining matches is unlikely to happen. And it is more likely to happen in the beginning and the end of a match, instead of the middle.
Not all outcomes could happen as the same results as flipping a coin, there’s also other factors that we should put under consideration. But the experiment nevertheless, relevant to sports betting.